勉強お役立ちコラム

自分で偏差値を求めよう！受験に上手く活用しよう

受験する高校を考えるとき、偏差値を基準にすることが多いですよね。

今回は、自分で求められる偏差値の具体的な計算方法を、みなさんの受験に活用できるようにお伝えしていきます！

ベスト個別では、毎年HPで予想偏差値を公開しています。

受験校選びの際に参考にしていただければと思います。

この記事では、偏差値の具体的な計算方法をお伝えします。

カンタンに「偏差値とは何なのか？」「注意点はどんなところなのか？」を知りたい方は、こちらの記事をご覧ください。

偏差値は、次の公式で求めることができます。

この公式を見て、「標準偏差…！？難しいかも…」と思った方、安心してください。この公式は使いません。

というのも、この公式、特に標準偏差はテストを受けた全員の点数が分からなければ求められないので、個人で使うにはハードルが高すぎるのです。

そして今回のテーマは、“自分で求められる”偏差値の計算方法です！

自分でも求められる偏差値の計算式は、次の通りです。

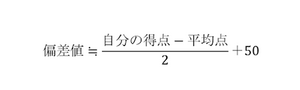
この計算式なら、自分の得点と平均点さえ分かれば自分で偏差値を出すことができますよね。

みなさんも、自分の偏差値を計算してみてください！

ですが、式が簡単になった分、注意点もあるのでお伝えします。

それは、この計算で出せる偏差値は、「だいたい正確」ということです。

実際に数値を入れて上の公式と比較すると、だいたい±2くらいの誤差が出ます。

ですので、この計算式で出した偏差値は、だいたいの自分の位置を掴むための参考として活用するようにしましょう。偏差値1、2の差が重要な局面での使用はオススメできません。

またカンタンに分かる偏差値の特徴と注意点？でも書いた通り、正確な偏差値を知りたい場合はなるべく受験本番に近い模試の偏差値を参考にしましょう。高校受験であれば県内の中3生がより多く受ける模試、大学受験であれば全国の高3生などがより多く受ける模試の偏差値が信憑性が高いものとなります。

いかがでしたか？

自分で正確に偏差値を計算するのはテストを受けた全員の得点が必要となるため少し難しいですが、今回お伝えした方法であれば、おおよその偏差値を求めることができます。

自分の偏差値を正しく知り、受験校選びにしっかり活かしていきましょう！